Question

What is the behaviour near horizontal asymptotes of this curve? And what is the behaviour near vertical asymptotes of this curve? - image attached (if possible, please find range as well)

Answer 1

Let's start with the range. The range of the function is every real number except such that values that makes the denominator turns into zero. To find these values, we have to find the factors of the deniminator.

In this case, we have to look for two numbers a*b= -12 and a+b= -1 . (Other way to do this part is using the quadratic formula).

By solving this part we find that:

`x^2-x-12=(x+3)(x-4)`

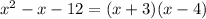
Then, the domain is every real number except -3 and 4. These two values are also the vertical asymptotes. The vertical asymptotates are:

`\begin{gathered} x=-3 \\ x=4 \end{gathered}`

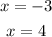
Now the horizontal asymptotes are the limits of the function when x goes to infinity:

`\lim_(x\to\infty)(2x^2-3x)/(x^2-x-12)`

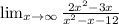
Here, to solve this limit we divide the numerator and the denominator by x^2:

If we evaluate x as infinity, we got:

Then, there is one horizontal asymptote which is y=2.

Now, to find the range we have to solve for x. First we multiply each side of the function by (x^2-x-12) as follows:

`\begin{gathered} f(x)=y \\ y=(2x^2-3x)/(x^2-x-12) \\ \left(x^2-x-12\right)*y=2x^2-3x \end{gathered}`

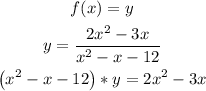
Now we group the terms:

`\begin{gathered} x^2y-xy-12y-2x^2+3x=0 \\ x^2(y-2)+x(3-y)-12y=0 \end{gathered}`

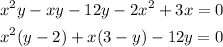
Now we apply the quadratic formula, where a=(y-2), b=3-y, and c=-12y.

`\begin{gathered} x=(-b\pm√(b^2-4ac))/(2a) \\ x=(-3+y\pm√(9-6y+y^2-4(y-2)(-12y)))/(2(y-2)) \end{gathered}`

Operating:

`\begin{gathered} x=(-3+y\pm√(9-6y+y^2+48y^2-96y))/(2y-4) \\ x=(-3+y\pm√(49y^2-102y+9))/(2y-4) \end{gathered}`

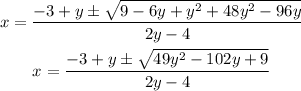
Now he know that the discriminant should be greater or equal than zero.

`49y^2-102y+9\ge0`

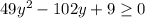
To solve this inequality, first we complete the square:

`49(y-(51)/(49))^2-(2160)/(49)\ge0`

Now we add 2160/49 to both sides:

`49(y-(51)/(49))^2\ge(2160)/(49)`

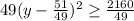
We divide both sides by 49:

`(y-(51)/(49))^2\ge(2160)/(2401)`

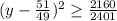
Now:

`\begin{gathered} y-(51)/(49)\leq-\sqrt{(2160)/(2401)}\text{ or:} \\ y-(51)/(49)\ge\sqrt{(2160)/(2401)} \end{gathered}`

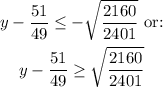
Operating the roots and solving for "y" we got:

`\begin{gathered} y\leq(-12√(15)+51)/(49)\text{ or:} \\ y\ge(12√(15)+51)/(49) \end{gathered}`

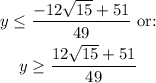
Finally, the range is:

`(-\infty,(-12√(15)+51)/(49)\rbrack\text{ }\cup\text{ }\lbrack(12√(15)+51)/(46),\text{ }\infty)`