Given:
The sum of the base and height of a triangle is 12cm.
To find:
The largest possible area of the triangle.
Step-by-step explanation:
According to the problem,
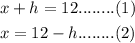
Using the area formula of the triangle,
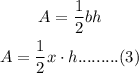
Substituting equation (2) in (3),
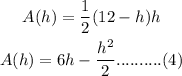
Using the first derivative test,

Since,
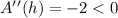
So, it has a maximum value of h = 6.
Substituting h = 6 in equation (2) we get,

Therefore, the largest possible area will be,

Final answer:
The largest possible area of the triangle is 18 square cm.