The expression
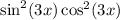 in terms of cosines is
in terms of cosines is

How to rewrite the expression in terms of cosines
From the question, we have the following parameters that can be used in our computation:
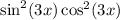
The sin and cosine identity represented as
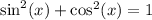
So, we have
![\sin^2(3x)\cos^2(3x) = [1 - \cos^2(3x)]\cos^2(3x)](https://img.qammunity.org/2023/formulas/mathematics/college/p8vj15etdlu601z6vlsj4wh29f5l2or4sh.png)
Expand the equation
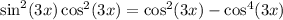
Hence, the expression in terms of cosines is
