We are given that a city has a population of 136000 in 1992 and a growth rate of 1.7% per year.
Part a) An exponential function that models the exponential growth is given by:
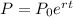
Where
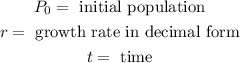
The growth rate in decimal form is the following:
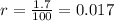
Now we substitute the values and we get:
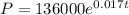
Part b) For the year 2005 there are 13 years, therefore, we substitute in the equation the values t = 13:
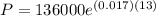
Solving the operations we get:
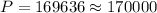
Therefore, the population in 2005 is approximately 170000.