Question

The population of a city was 136 thousand in 1992. The exponential growth rate was 1.7% per year.a) Find the exponential growth function in terms of t, where t is the number of years since 1992.P(t) = 136,000 e 0.0177b) Predict the population in 2005, to the nearest thousand.(Round to the nearest thousand as needed.)

Answer 1

We are given that a city has a population of 136000 in 1992 and a growth rate of 1.7% per year.

Part a) An exponential function that models the exponential growth is given by:

`P=P_0e^(rt)`

Where

`\begin{gathered} P_0=\text{ initial population} \\ r=\text{ growth rate in decimal form} \\ t=\text{ time} \end{gathered}`

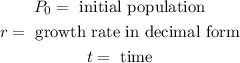
The growth rate in decimal form is the following:

`r=(1.7)/(100)=0.017`

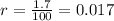
Now we substitute the values and we get:

`P=136000e^(0.017t)`

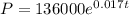
Part b) For the year 2005 there are 13 years, therefore, we substitute in the equation the values t = 13:

`P=136000e^((0.017)(13))`

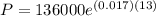
Solving the operations we get:

`P=169636\approx170000`

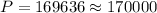
Therefore, the population in 2005 is approximately 170000.