Question

I need help with this question... the correct answer choice

Answer 1

Given

The coordinates of the triangle ABC are:

`\begin{gathered} A\mleft(-2,-2\mright) \\ B(-6,\text{ -3)} \\ C(-1,\text{ -6)} \end{gathered}`

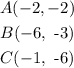
The coordinates of the triangle DEF are:

`\begin{gathered} D(2,\text{ 2)} \\ E(6,\text{ 3)} \\ F(1,\text{ 6)} \end{gathered}`

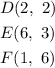
The sequence of transformation that maps triangle ABC onto triangle DEF is

1. Reflection over the x-axis

The rule for the reflection over the x-axis:

`(x,\text{ y) }\rightarrow\text{ (x, -y)}`

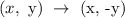
Applying this rule to the triangle ABC gives:

`\begin{gathered} A^(\prime)(-2,\text{ 2)} \\ B^(\prime)(-6,\text{ 3)} \\ C^(\prime)(-1,\text{ 6)} \end{gathered}`

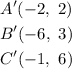
2. Reflection over the y-axis:

The rule for the reflection over the y-axis:

`(x,\text{ y) }\rightarrow\text{ (-x, y)}`

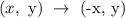
Applying this gives :

`\begin{gathered} A^(\prime)(-2,\text{ 2) }\rightarrow\text{ D(2, 2)} \\ B^(\prime)(-6,\text{ 3) }\rightarrow\text{ E(6, 3)} \\ C^(\prime)(-1,\text{ 6) }\rightarrow\text{ F(1, 6)} \end{gathered}`

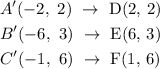
Hence, the correct option is option A