Question

Solve for X and Y. Then find the perimeter of the triangle. Round your answers to the nearest tenth.

Answer 1

Given that the triangle is a right triangle, where x is the side opposite the given angle and y is the longest sides (hypotenuse).

The given side length which is the adjacent = 14 feet.

Given angle, Θ = 25 degrees

Let's solve for x and y.

To find x, use the formula below:

`\tan \theta=(x)/(14)`

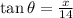
Thus, we have:

`\begin{gathered} x=14\tan 25 \\ \\ x\text{ = }6.5\text{ ft} \end{gathered}`

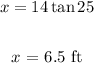
To solve for y, use pythagoras theorem:

`\begin{gathered} y=\sqrt[]{6.5^2+14^2} \\ \\ y=\sqrt[]{42.25+196} \\ \\ y=\sqrt[]{238.25} \\ \\ y=15.44\text{ ft} \end{gathered}`

To find the perimeter of the right triangle, use the formula below:

`P=x+y+z`

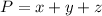
Where z = 14 ft

Now input values into the formula:

`P=6.5^{}+14^{}+15.4\text{ = 35}.9\text{ ft}`

The perimeter is 35.9 ft

ANSWER:

x = 6.5 ft

y = 15.4 ft

Perimeter = 35.9 ft