Given:
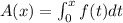
The graph of f(x) is shown.
Let's find the following:
• (a). At what x value does A(x) have a local max?
The local maxima are the points where the function has a maximum value.
We have:
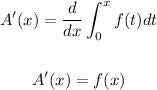
Using the graph, when f(x) =0, the values of x are:
x = 1, 3, 5
Which means the critical points are:
x = 1, 3, and 5
Now, let's apply the first derivative test which states that when A'(x) changes from negative to positive there is a local minimum at that point while when A'(x) changes from positive to negative, there is a local maximum at that point.
Using the graph, we have the following:
The change from negative to positive occur at: x = 1, 5. This means the local min occurs at these points.
The change from positive to negative occur at: x = 3. Hence, the local max occurs at this point.
ANSWER:
• Local max: x = 3
• Local min: x = 1, 5