The answer is: " $0.67 / metre " ;
or, write as: " [
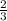 dollar] per metre."
dollar] per metre."
____________________
Explanation:
This is a unit rate problem:
Find the cost in dollars per [single unit—in this case: "metre(s)", "m" ;
_________________
 ; Solve for the "?" amount of dollars.
; Solve for the "?" amount of dollars.
_________________
Method 1) "Cross-factor multiply" :
Note: Given: "
![(a)/(b) = (c)/(d) ; [b\\eq 0; d\\eq 0]](https://img.qammunity.org/2023/formulas/mathematics/college/xbvaxzieqy2u3fk8jtar9pjnrz1ar9dgtg.png) " ;
" ;
then: ⟷ "
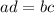 " ;
" ;
_________________
So: " \frac{200 dollars}{300m} = \frac{? dollars}{1m} " ;
then: ⟷ " (200*1) = (300* ?) ;
→ " (200) = (300 * ?)" ;
↔ " (300 * ?) = 200 " ;
Let "x" refer to the "?" ; the "unknown value" (in dollars);
for which we are trying to solve.
⇒ " 300x = 200 " ; Solve for "x" ;
→ Divide each side of the equation by: "300" ;
to isolate "x" on the "left-hand side" of the equation; & to solve for "x" ;
⇒ 300x/ 300 = 200/300 ;
To get: " x =
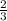 dollars" ;
dollars" ;
= $0.666666666... ;
round to: $0.67 .
{since: " 1 dollar = $1.00 = 100 cents" ;
and since: "\frac{2}{3} " ;
= ["2 ÷ 3" = 0.666666...." ] ;
⇒ round to: "0.67 " ;
and write as:
__________
⇒ $0.67 / metre ; or, write as:
" [
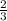 dollar] per metre."
dollar] per metre."
_________
Method 2) Note:
\frac{200 dollars}{300m} = \frac{? dollars}{1m} ;
⇔ = "
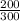
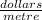 " ;
" ;
{Note: "[200÷300]" can be simplified by "canceling out" the two (2) zeros in both the numerator and the denominator.}.
= " \frac{2 dollars}{3m} ";
_________
= i.e. "
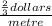 " or;
" or;
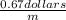 ; or: $0.67 / metre .
; or: $0.67 / metre .
⇒ {since: "
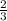 of 1 dollar" = " \frac{2}{3} dollars of 100 cents" ;
of 1 dollar" = " \frac{2}{3} dollars of 100 cents" ;
⇒ {since: "1 dollar = 100 cents"} ;
⇒ {and: "
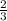 " = 0.6666666666666... " } ;
" = 0.6666666666666... " } ;
→ round to: "0.67 " ; and thus: $0.67 / metre.
_________
Note that using either of these 2 (two) methods result in the same answer.
Hope this is helpful! Best wishes to you within your academic pursuits!
_________________