Let n = 25, p = 0.4, q = 1-0.4=0.6.
The formula for the binomial probability is as follows:
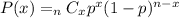
To obtain the probability of at least 10, solve for P(10)+P(11)+P(12)+...+P(25).
Thus, we have the following.
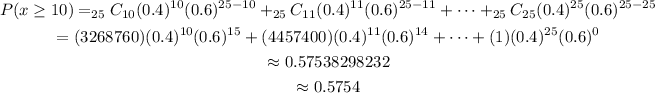
Therefore, the probability that at least 10 of them prefer the news online is approximately 0.5754 or 57.54%.