Step-by-step explanation
The symbol Σ (called sigma) means "sum up". So, in this case, the expression indicates the sum of the (xᵢ)², where i goes from 1 to 4, which is 1, 2, 3 and 4. Then, we have:
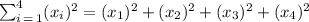
From the word problem, we know the value of each xᵢ.
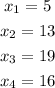
Finally, we operate.
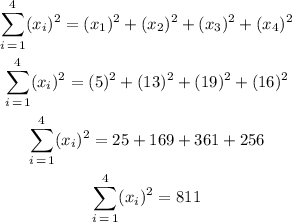
Answer
The result of computing the given expression is 811.