Question

The ratio of the radius of two distinct spheres is 3:4. What is the ratio of their respective surface areas?A. 27:64B. 4:3C. 9:16D. 3:4

Answer 1

Given that the ratio of the radius of two distinct spheres is;

`3\colon4`

The surface area of a sphere is;

`A=4\pi* r^2`

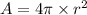
Thus, the surface area of the first sphere is;

`\begin{gathered} A_1=4\pi(3)^2 \\ A_1=36\pi \end{gathered}`

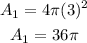
Similarly, the surface area of the second sphere is;

`\begin{gathered} A_2=4\pi(4)^2 \\ _{}A_2=64\pi \end{gathered}`

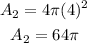
Hence, the ratio of the surface areas is;

`(A_1)/(A_2)=(36\pi)/(64\pi)`

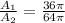
Reducing the fraction, we have;

`\begin{gathered} (A_1)/(A_2)=(9)/(16) \\ A_1\colon A_2=9\colon16 \end{gathered}`

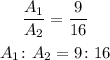
CORRECT OPTION: C