Question

Two fractions have denominators of x^2+ 6x + 9 and x^2. What is the Least Common Denominator?

Answer 1

Write out the denominator of the fraction, we have

`\begin{gathered} x^2+6x+9 \\ \text{And } \\ x^2-9 \end{gathered}`

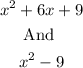
We want to obtain the least common denominator.

To do this, we need to factorize each of the expression given

`\begin{gathered} x^2+6x+9 \\ =x^2+3x+3x+9 \\ =x(x+3)+3(x+3) \\ =(x+3)(x+3) \end{gathered}`

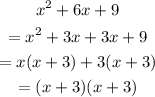
Then we factorise the other fraction using difference of two square

`\begin{gathered} a^2-b^2=(a-b)(a+) \\ \text{Then} \\ x^2-9=x^2-3^2 \\ =(x-3)(x+3) \end{gathered}`

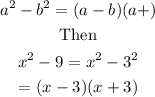
The the factorise expression becomes

`(x+3)(x+3)\text{ and (x-3)(x+3)}`

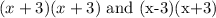
To obtain the least common denominator, we select the common factor and the product of the other factor,

Hence

`\begin{gathered} \text{common factor=(x+3)} \\ \text{The other factors are (x-3)(x+3)} \\ \text{Then } \\ \text{Least co}mmon\text{ denominator becomes } \\ (x+3)(x-3)(x+3) \end{gathered}`

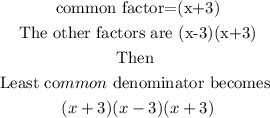
Thus

The Least Common Denominator is (x +3)(x+3)(x-3) (Last Option )