SOLUTION
Write out the denominator of the fraction, we have

We want to obtain the least common denominator.
To do this, we need to factorize each of the expression given
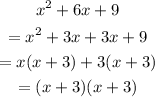
Then we factorise the other fraction using difference of two square
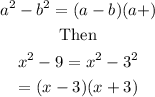
The the factorise expression becomes
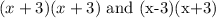
To obtain the least common denominator, we select the common factor and the product of the other factor,
Hence

Thus
The Least Common Denominator is (x +3)(x+3)(x-3) (Last Option )