Question

Simple pendulum calculation expert A simple pendulum with a period of 2.0s has it length doubled. Its new time period will be ?

Answer 1

Given that the time period of the pendulum is T = 2 s

Let the length of the pendulum be L.

The new length of the pendulum is 2L

The relation between length and time period is

`T=2\pi\sqrt[]{(L)/(g)}`

Here, g = 9.8 m/s^2 is the acceleration due to gravity.

The length will be

`\begin{gathered} L=(T^2)/(4\pi^2)* g \\ =((2)^2)/(4*(3.14)^2)*9.8 \\ =\text{ 0.994 m} \end{gathered}`

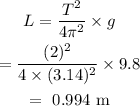
The new length will be

`\begin{gathered} 2L=2*0.994 \\ =1.988\text{ m} \end{gathered}`

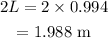
The new length will be 1.988 m

The new time period will be

`\begin{gathered} T^(\prime)=2\pi\sqrt[]{(2L)/(g)} \\ =2*3.14*\sqrt[]{(1.988)/(9.8)} \\ =2.83\text{ s} \end{gathered}`

Thus, the new time period is 2.83 s