Given that the time period of the pendulum is T = 2 s
Let the length of the pendulum be L.
The new length of the pendulum is 2L
The relation between length and time period is
![T=2\pi\sqrt[]{(L)/(g)}](https://img.qammunity.org/2023/formulas/physics/college/h8quhyohkhg6oj9xkblumno6z1ebdjigmr.png)
Here, g = 9.8 m/s^2 is the acceleration due to gravity.
The length will be
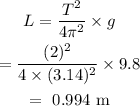
The new length will be
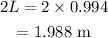
The new length will be 1.988 m
The new time period will be
![\begin{gathered} T^(\prime)=2\pi\sqrt[]{(2L)/(g)} \\ =2*3.14*\sqrt[]{(1.988)/(9.8)} \\ =2.83\text{ s} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/kkz8l3oi5z6aq3eb0rq6rflr1ibj9g0rxy.png)
Thus, the new time period is 2.83 s