Find the measure of an angle whose supplement is six times its complement. Hint: The supplement and complement of an angle are (180 - 0)° and (90 – 6)º respectively.

Question

asked Nov 17, 2023 122k views

1 Answer

DougN · Answer 1 · 2023-11-20T15:00:10+0000

Let us translate the statements in the problem to mathematics equations

Let the angle is x degree

So its supplement is

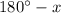
$180^(\circ)-x$

And its complement is

$90^(\circ)-x$

Since the supplement is 6 times its complement, so Multiply the complement by 6 and equate the answer by the supplement

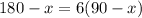
Let us simplify the right side

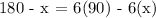
$180\text{ - x = 6(90) - 6(x)}$
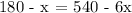
$180\text{ - x = 540 - 6x}$

Now let us solve the equation to find x

At first, add 6x to both sides to put x in the left side

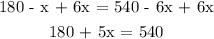
$\begin{gathered} 180\text{ - x + 6x = 540 - 6x + 6x} \\ 180\text{ + 5x = 540} \end{gathered}$

Now subtract 180 from both sides to put the number in the right side

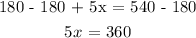
$\begin{gathered} 180\text{ - 180 + 5x = 540 - 180} \\ 5x\text{ = 360} \end{gathered}$

Divide both sides by 5 to get x

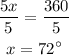
$\begin{gathered} (5x)/(5)=(360)/(5) \\ x=72^(\circ) \end{gathered}$

So the measure of the angle is 72 degrees

You can check the answer

180 - 72 = 108

90 - 72 = 18

18 * 6 = 108

So the supplement of 72 is six times its complement