We are given the following geometric sequence
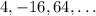
Let us first find a general formula for this sequence then we can easily find the 13th term.
Recall that a geometric sequence is given by
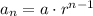
Where aₙ is the nth term, a is the first term and r is the common ratio
The common ratio can be found by dividing the consecutive terms of the sequence.
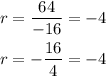
So the common ratio is -4 and the first term is 4
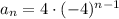
The above is the general formula for the sequence.
Now to find the 13th term, substitute n = 13 into the above formula
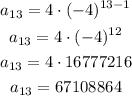
Therefore, the 13th term of the sequence is 67,108,864