Question

Given a 30-60-90 triangle whose shortest leg is 3 centimeters, what is the length of the hypotenuse?1.5 cm32 cm3V3cm6 cm.

Answer 1

6 cm

Explanation:

When a triangle has the measurements 30-60-90, it has the following form (depending on the shortest leg):

Confirmed by the Pythagorean Theorem

`\begin{gathered} \mleft(2a\mright)^2=a^2+\mleft(a√(3)\mright)^2 \\ 4a^2=a^2+3a^2 \\ 4a^2=4a^2 \end{gathered}`

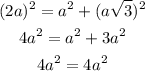
Therefore:

If the value of a is equal to 3, the hypotenuse would be:

`2a=2\cdot3=6`

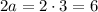
The value of the hypotenuse is 6 cm