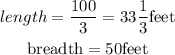Question

A Gardener has 400 feet of fencing to enclose three adjacent vegetable plots. What dimensions should be used so that the enclosed area will be a maximum?Answer and explanation please.

Answer 1

Given:

The perimeter of the fencing is 400 feet.

Each plot is assumed to be a rectangle.

The three adjacent plots are as sketched below;

The perimeter of the 3plots is given by the addition of all the sides;

Hence,

`P=6l+4b`

Hence,

`\begin{gathered} 6l+4b=400 \\ \\ \text{Thus,} \\ 4b=400-6l \\ b=(400-6l)/(4) \\ b=100-(3l)/(2)\ldots\ldots\ldots\ldots\ldots.\ldots\ldots(1) \end{gathered}`

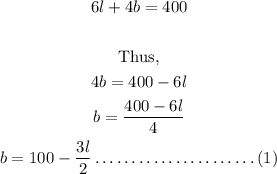
The area of a rectangle is given by;

`A=l* b`

Substituting the breadth in equation (1) into the formula for area,

`\begin{gathered} A=l* b \\ A=l(100-(3l)/(2)) \\ A=100l-(3l^2)/(2) \end{gathered}`

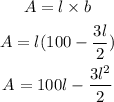
To get the maximum area, we differentiate the area with respect to l and equate to zero to find the critical points.

`\begin{gathered} A=100l-(3l^2)/(2) \\ A^(\prime)=100-3l^{} \\ \text{Equating A' = 0} \\ 100-3l=0 \\ 100=3l \\ l=(100)/(3) \end{gathered}`

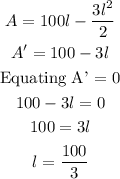
Thus,

`\begin{gathered} b=100-(3l)/(2) \\ b=100-((3)/(2)*(100)/(3)) \\ b=100-50 \\ b=50 \end{gathered}`

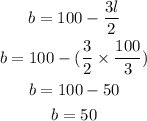
Since the second derivative is a negative, then the first derivative = 0 guarantees a maximum.

Also, the coefficient of l-square is negative, this also guarantees a maximum point.

`\begin{gathered} A=100l-(3l^2)/(2) \\ \text{Considering quadratic function of the form:} \\ ax^2+bx+c=0 \\ \text{when a < 0, then a max imum occurs} \\ \text{Hence, for the area, } \\ a=-(3)/(2) \\ \text{Thus it will have a max imum point} \end{gathered}`

`\begin{gathered} A^(\prime)=100-3l \\ A^(\doubleprime)=-3 \\ \\ \text{Hence, } \\ A^(\prime)=0\text{ is where the max imum point occurs} \end{gathered}`

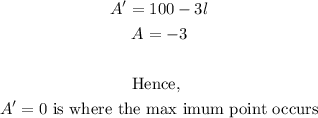
Hence, the dimensions needed to get a maximum area for the plots will be;

`\begin{gathered} length=(100)/(3)=33(1)/(3)\text{feet} \\ \text{breadth}=50\text{feet} \end{gathered}`