Question

Given by and vwz,what is the perimeter of the trapezoid WXYZ ..

Answer 1

We are given two similar triangles, therefore, we have the following relationship:

`(VZ)/(ZY)=(VW)/(WX)`

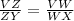
Solving for VW:

`VW=WX*(VZ)/(ZY)`

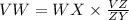
Replacing in the equation:

`VW=36*((44-27.5))/(27.5)`

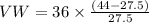
Solving the operations:

`VW=21.6`

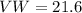
Now we use the Pythagorean theorem to determine the length of WZ, that is:

`WZ=\sqrt[]{(VW)^2-(VZ)^2}`

Replacing:

`WZ=\sqrt[]{(21.6)^2-(44-27.5)^2}`

Solving the operations:

`\begin{gathered} WZ=\sqrt[]{466.56-272.25} \\ WZ=\sqrt[]{194.31} \\ WZ=13.9 \end{gathered}`

Now we find XY using the following relationship:

`(XY)/(VY)=(WZ)/(VZ)`

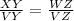
Solving for XY:

`XY=VY*(WZ)/(VZ)`

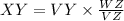
Replacing the values:

`XY=44*(13.9)/(44-27.5)`

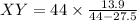
Solving the operations:

`XY=37.1`

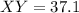
The perimeter of the figure is:

`P=XW+WZ+ZY+XY`

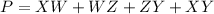
Replacing:

`P=36+13.9+27.5+37.1`

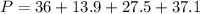
Solving the operations:

`P=114.5`