Answer:
36.1 feet.
Step-by-step explanation:
From the diagram:
• The side length ,opposite ,angle 31° = x
,
• The side length ,adjacent to ,angle 31° = 60
Recall from trigonometry that:
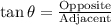
This implies that:
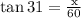
Cross multiply:
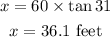
The length of HI is 36.1 feet (to the nearest tenth of a foot).