Given: The graph of the function below:
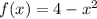
To Determine: The equation of the tangent line to the given graph at the point
(-1, 3), at (0, 4), and at (5, -21)
Determine the slope of the given expression
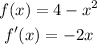
The slope at the point (-1, 3) would be
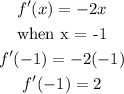
Find the line with slope 2 passing through the point (-1, 3).
The equation of a line given the slope and the point is given by the formula below:
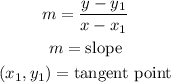
So, the equation would be

Hence, the equation of the tangent to the graph at the point (-1, 3) is
y = 2x+5
Find the slope at the point (0, 4).
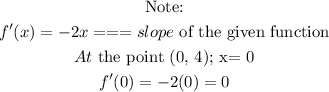
Find the equantion of the line with slope o passing through the point (0, 4)
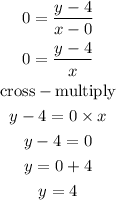
Hence, the equation of the tangent to the graph at the point (0, 4) is
y = 4
Find the slope at the point (5, -21)
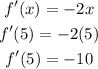
Use the slope -10 and the tangent point (5, -21) to calculate the equation of the tangent
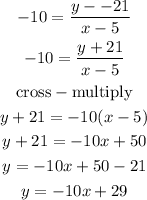
ANSWER SUMMARY
The equation of the tangent line to the given graph at:
the point (-1, 3) is y = 2x+5
the point (0, 4) is y = 4
the point (5, -21) is y = -10x + 29