Question

Find an equation of the tangent line to the graph of f(x) = 4-x^2 at the point (1,-3), at (0,4), and at (5,-21).

Answer 1

Given: The graph of the function below:

`f(x)=4-x^2`

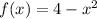
To Determine: The equation of the tangent line to the given graph at the point

(-1, 3), at (0, 4), and at (5, -21)

Determine the slope of the given expression

`\begin{gathered} f(x)=4-x^2 \\ f^(\prime)(x)=-2x \end{gathered}`

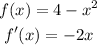
The slope at the point (-1, 3) would be

`\begin{gathered} f^(\prime)(x)=-2x \\ \text{when x = -1} \\ f^(\prime)(-1)=-2(-1) \\ f^(\prime)(-1)=2 \end{gathered}`

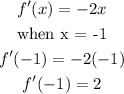
Find the line with slope 2 passing through the point (-1, 3).

The equation of a line given the slope and the point is given by the formula below:

`\begin{gathered} m=(y-y_1)/(x-x_1) \\ m=\text{slope} \\ (x_1,y_1)=\text{tangent point} \end{gathered}`

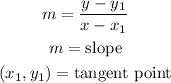
So, the equation would be

`\begin{gathered} f^(\prime)(-1)=2=\text{slope} \\ (-1,3)=\text{tangent point} \\ 2=(y-3)/(x--1) \\ 2=(y-3)/(x+1) \\ \text{cross}-m\text{ultiply} \\ y-3=2(x+1) \\ y-3=2x+2 \\ y=2x+2+3 \\ y=2x+5 \end{gathered}`

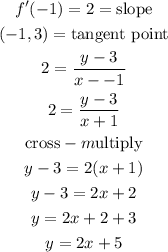
Hence, the equation of the tangent to the graph at the point (-1, 3) is

y = 2x+5

Find the slope at the point (0, 4).

`\begin{gathered} \text{Note:} \\ f^(\prime)(x)=-2x===slope\text{ of the given function} \\ At\text{ the point (0, 4); x= 0} \\ f^(\prime)(0)=-2(0)=0 \end{gathered}`

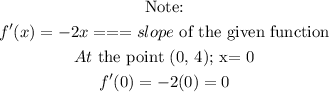
Find the equantion of the line with slope o passing through the point (0, 4)

`\begin{gathered} 0=(y-4)/(x-0) \\ 0=(y-4)/(x) \\ \text{cross}-\text{multiply} \\ y-4=0* x \\ y-4=0 \\ y=0+4 \\ y=4 \end{gathered}`

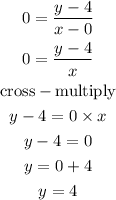
Hence, the equation of the tangent to the graph at the point (0, 4) is

y = 4

Find the slope at the point (5, -21)

`\begin{gathered} f^(\prime)(x)=-2x \\ f^(\prime)(5)=-2(5) \\ f^(\prime)(5)=-10 \end{gathered}`

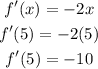
Use the slope -10 and the tangent point (5, -21) to calculate the equation of the tangent

`\begin{gathered} -10=(y--21)/(x-5) \\ -10=(y+21)/(x-5) \\ \text{cross}-\text{multiply} \\ y+21=-10(x-5)_{} \\ y+21=-10x+50 \\ y=-10x+50-21 \\ y=-10x+29 \end{gathered}`

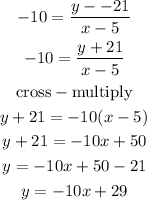
ANSWER SUMMARY

The equation of the tangent line to the given graph at:

the point (-1, 3) is y = 2x+5

the point (0, 4) is y = 4

the point (5, -21) is y = -10x + 29