From the doorframe we can take a triangle with the corresponding measures
we realize, it is like a right triangle then if we use pythagoras and the measures match the red angles and the other angles of the doorframe must be right
we use the hight(81) and width(32.5) to find the hypotenuse (87)
Pythagoras
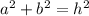
where a and b are legs of the triangle and h the hypotenuse
then repalcing
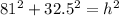
simplify

and solve for the hypotenuse
![h=\sqrt[]{7617.25}\approx87.3](https://img.qammunity.org/2023/formulas/mathematics/college/oq0y7ez7bxnazwyegmh5ut8rjuwnoyoh10.png)
the measure of the hypotenuse is 87.3in and the measure of the diagonal of the door is 87in.
By allow of measurement and rounding errors we can say the values are the same, then the corners of the door are right and the doorframe is square