Answer:

Explanations:
The given functions can be generalized using the form f(x) = y
Given the following functions;
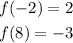
These functions can be written as coordinates points (-2, 2) and (8, -3)
The equation of the linear function in slope-intercept form is expressed as y = mx + b
m is the slope:
b is the y-intercept
Get the slope of the line passing through the points:
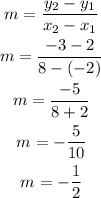
Get the y-intercept using the point(-2, 2) and m = -0.5
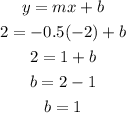
Write the equation in slope-intercept form where m = -0.5 and b = 1;
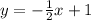
Write in point-slope form;
The point-slope form of the equation is expressed as;

Using the following parameters;
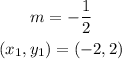
Substitute the given parameters into the point-slope form of the equation;
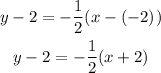
This gives the point-slope form of the equation.
For the standard form:
The standard form of the linear equation is expressed as:
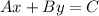
Recall that;
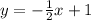
Rearrange in standard form as shown:
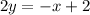
Add "x" to both sides of the equation:

This gives the required linear equation in standard form.