Question

A motorboat can maintain a constant speed of 37 miles per hour relative to the water. The boat makes a trip upstream to a certain point in 47 minutes; the return trip takes 27 minutes. What is the speed of the current?

Answer 1

We have to find the speed of the current (Vc).

We now that a trip upstream took 47 minutes (47/60 hours, with the current against the movement of the boat) and a trip downstream took 27 minutes (27/60 hours).

The speed of the boat is constant with a value of Vb = 37 miles per hour.

As the average speed is equal to the distance divided by the time, we can write for the trip upstream:

`V_b-V_c=(d)/(t)=(d)/(47\/60)=(60)/(47)d`

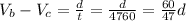
For the trip downstram the current is in favor of the boat so we can write:

`V_b+V_c=(d)/(t)=(d)/(27\/60)=(60)/(27)d`

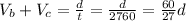
We can then add the two equations as:

`\begin{gathered} V_b-V_c+(V_b+V_c)=(60)/(47)d+(60)/(27)d \\ 2V_b=60d((1)/(47)+(1)/(27)) \\ 2\cdot37=60d\cdot((27+47)/(47\cdot27)) \\ 74=60d((74)/(1269)) \\ d=(74\cdot1269)/(74\cdot60) \\ d=21.15\text{ }miles \end{gathered}`

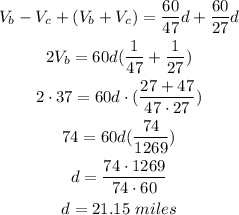
Knowing the distance d = 21.15 miles, we can find the speed of the current as:

`\begin{gathered} V_b+V_c=(60d)/(27) \\ V_c=(60d)/(27)-V_b \\ V_c=(60\cdot21.15)/(27)-37 \\ V_c=47-37 \\ V_c=10\text{ }mph \end{gathered}`

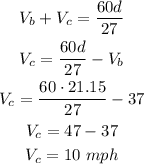
Answer: the speed of the current is 10 miles per hour.