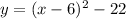 Step-by-step explanation
Step-by-step explanationgiven

The vertex form is a special form of a quadratic function. From the vertex form, it is easily visible where the maximum or minimum point (the vertex) of the parabola is, it has the form
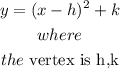
Step 1
a) complete the square
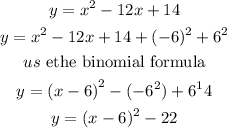
so , the equation in vertex form is
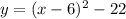
I hope this helps you