Question

If 3000 dollars is invested in an account for 10 years. Find the value of the investment at the end of10 years if the interest is:(a) 6.2% compounded annually: $(b) 6.2% compounded semiannually: $(c) 6.2% compounded quarterly: $(d) 6.2% compounded monthly: $(e) 6.2% compounded daily (ignore leap years): $Round answers to the nearest cent.

Answer 1

(a) 6.2% compounded annually: $5474.78

(b) 6.2% compounded semiannually: $5524.52

(c) 6.2% compounded quarterly: $5550.32

Explanation:

For an investment at compound interest, the value of the investment at the end of t years is calculated using the formula:

`A(t)=P\left(1+(r)/(k)\right)^(tk)\text{ where }\begin{cases}P=\text{Principal Invested} \\ r=\text{Interest Rate} \\ k=\text{Number of compounding periods}\end{cases}`

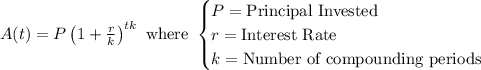
Given:

• Principal Amount = $3,000

,

• Time = 10 years

(a)6.2% compounded annually

• Rate = 6.2% = 0.062

,

• k=1 (Annually)

`\begin{gathered} A(10)=3000\left(1+(0.062)/(1)\right)^(10*1) \\ A(10)=\$5474.78 \end{gathered}`

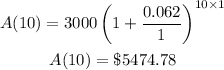
If the interest rate is 6.2% compounded annually, the value of the investment at the end of 10 years is $5474.78.

(b)6.2% compounded semiannually

• Rate = 6.2% = 0.062

,

• k=2 (semiannually)

`\begin{gathered} A(10)=3000\left(1+(0.062)/(2)\right)^(10*2) \\ A(10)=\$5524.52 \end{gathered}`

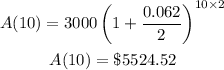
If the interest rate is 6.2% compounded semiannually, the value of the investment at the end of 10 years is $5524.52

Part C: 6.2% compounded quarterly

• Rate = 6.2% = 0.062

,

• k=4 (quarterly)

`\begin{gathered} A(10)=3000\left(1+(0.062)/(4)\right)^(10*4) \\ A(10)=\$5550.32 \end{gathered}`

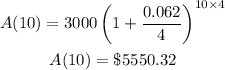
If the interest rate is 6.2% compounded quarterly, the value of the investment at the end of 10 years is $5,550.32

Part D: 6.2% compounded monthly