Question

Please answer this questionfind the distance iof the segment shown in the graph

Answer 1

To find the distance of the line segment you have to do as follows:

As you can see the line forms a right triangle with the x-axis as a base and the line parallel to the y-axis as its heigth

First determine the distance between both points over the x-axis, to determine the length of the base:

The first point has x-coordinate 4 and the second point has x-coordinate -5, subtract both coordinates to calculate the distance:

`b=4-(-5)=4+5=9`

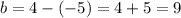
The base of the triangle is b=9 units

Second determine the distance between the poins iver the y-axis.

The y-coordinate for the first point is zero and the y-coordinate for the second point is 1, subtract the smaller from the greatest to determine the heigth of the triangle:

`h=1-0=1`

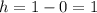
The height of the triangle is h=1 unit

Third, apply the Pythagoras theorem, wich states that for a rigth triangle the square of the hypothesunes is equal to the sum of squares of the base and heigth:

`\begin{gathered} a^2+b^2=c^2 \\ a=\text{base} \\ b=\text{height} \\ c=\text{hypothenuse} \end{gathered}`

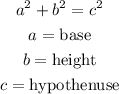
For this triangle it is:

`\begin{gathered} 9^2+1^2=c^2 \\ 81+1=c^2 \\ c^2=82 \\ c=\sqrt[]{82}=9.05 \end{gathered}`

The length of the segment shown in the graph is 9.05 units