Question

Writing an equation of a hyperbola given the Foci and asymptotes

Answer 1

Hello there. To solve this question, we'll have to remember some properties about foci and asymptotes of hyperbolas.

First, the equation for a hyperbola with real axis a and imaginary axis b is:

`((x-x_0)^2)/(a^2)-((y-y_0)^2)/(b^2)=1`

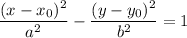
centered at (x0, y0) and axis of symmetry being the x-axis.

The asymptotes are given by the equations:

`y=\pm(b)/(a)x`

The relationship between a, b (the real and imaginary axis) and the value c (that stands for the coordinates of the foci)

`(-c,0)\text{ and }(c,0)`

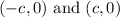
for hyperbolas is:

`c^2=a^2+b^2`

From the equation of the asymptotes, we find that:

`\begin{gathered} (b)/(a)x=7x \\ \\ (b)/(a)=7\Rightarrow b=7a \end{gathered}`

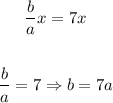
Hence we get:

`c^2=a^2+(7a)^2=a^2+49a^2=50a^2`

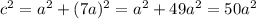
And from the coordinates of the foci, we get

`c=10`

Hence

`\begin{gathered} 10^2=50a^2 \\ 100=50a^2 \\ a^2=(100)/(50)=2\Rightarrow a=√(2) \end{gathered}`

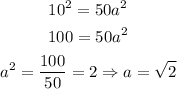
Then from the relation with b, we get

`b=7a=7√(2)`

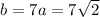
Finally, the center is the midpoint between the foci. In this case, we get:

`\begin{gathered} x_(center)=(-10+10)/(2)=0 \\ \\ y_(center)=(0+0)/(2)=0 \end{gathered}`

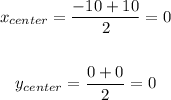
So we say the center is at the origin, or (x0, y0) = (0, 0).

Then we find the equation of the hyperbola:

`(x^2)/(2)-(y^2)/(98)=1`

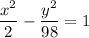
And with a software, you can see this is the right answer (see the following image:)

This is the answer to this question.