Step 1. The information that we have is:
The mean:
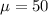
The standard deviation:
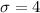
Step 2. To solve this problem and find what percent of scores are between 42 and 58, we use the empirical rule:
• The empirical rule for normally distributed data tells us that about 68% of the data falls under 1 standard deviation from the mean, about 95% falls under 2 standard deviations from the mean, and 99.7% of the data falls under 3 standard deviations from the mean.
Step 3. The following diagram represents the situation:
The marks on the graph are calculated as follows:
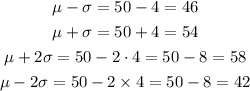
This is represented in the image:
Step 4. As you can see in the previous graph, 42 and 58 are 2 standard deviations away from the mean, this means that about 95% of the data will be between those values.
The option closest to 95% is B. about 95.4%
Answer: B. about 95.4%