Answer:(a) see equation below under point (a)
(b) The value for the denominator on x is: 1
(c) The value for the denominator on y is: 4
(d) The center is at the point = ( 0,0)
Explanations :
GIVEN :
4x^2 +y^2 = 4
This is of the form :
(x-a) ^2 =(y-b)^2 = r^2
where ( a;b) is the centere and r is the radius
The graph below show the x and y intercept and the centre of the graph 4x^2 +y^2 = 4
• This shows the centre ecclipses at (h;k) = (0;0) , b =2 and a = 1
(a) The standard form of the equation will be :
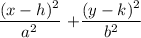
rewrite 4x^2 +y^2 = 4 in the standard ecclipse equation :
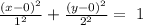
(b) The value for the denominator on x is: 1
(c) The value for the denominator on y is: 4
(d) The center is at the point = ( 0,0)