Mr Guny deposits $45,900 in a savings account
Principal, P = $45,900
Annual rate, R = 1.5%
Time, t = 1 year since it is componded quarterly,
Interest rate, r will be
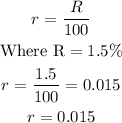
a) To find the first quarter's interest,
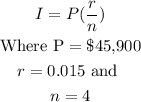
Substitute the values into the above expression
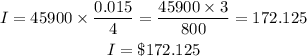
Hence, the first quarter's interest is $172.125
b) The first quarter's balance, A, will be
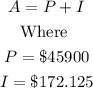
Substitute the values into the formula above
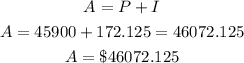
Hence, the first quarter's balance is $46,072.125