Given the function:
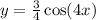
If we compare this to the general form:
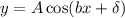
Where A is the amplitude, δ is the phase and b is a parameter, we identify:
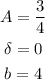
So the amplitude of the function is 3/4.
For the period, we need to remember that the period of a cosine function is 2π. Then:
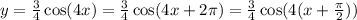
So the period of the function is π/2.