Question

Find the amplitude and period of the function. Y = 3/4 cos 4xGive the exact values, not decimal approximations.

Answer 1

Given the function:

`y=(3)/(4)\cos (4x)`

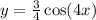
If we compare this to the general form:

`y=A\cos (bx+\delta)`

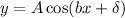
Where A is the amplitude, δ is the phase and b is a parameter, we identify:

`\begin{gathered} A=(3)/(4) \\ \delta=0 \\ b=4 \end{gathered}`

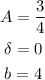
So the amplitude of the function is 3/4.

For the period, we need to remember that the period of a cosine function is 2π. Then:

`y=(3)/(4)\cos (4x)=(3)/(4)\cos (4x+2\pi)=(3)/(4)\cos (4(x+(\pi)/(2)))`

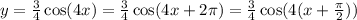
So the period of the function is π/2.