ANSWER
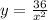
Step-by-step explanation
We want to find the equation that describes the relationship of the given variables.
y varies inversely as the square of x. This implies that:
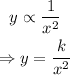
where k = constant of proportionality
When x = 3, y = 4. Substitute that into the equation above and solve for k:

Hence, the equation that represents the relationship of the variables is:
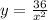
That is the answer.