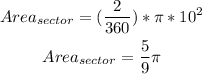Answer:
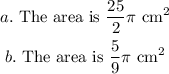
Explanation:
The area of a circle is represented by the following equation;
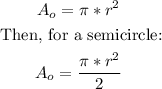
Therefore, for a semicircle with a radius of 5cm:
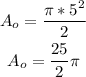
The area of the sector is given as:
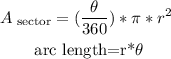
Given the arc length and the radius, solve for the angle:
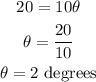
Now, for the area of the sector: