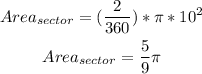Question

Find the area of the semicircle and thesector shown to the right. Leave youranswers in terms of I.

Answer 1

`\begin{gathered} a.\text{ The area is }(25)/(2)\pi\text{ cm}^2 \\ b.\text{ The area is }(5)/(9)\pi\text{ cm}^2 \end{gathered}`

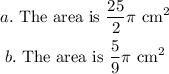
Explanation:

The area of a circle is represented by the following equation;

`\begin{gathered} A_o=\pi *r^2 \\ \text{ Then, for a semicircle:} \\ A_o=(\pi *r^2)/(2) \end{gathered}`

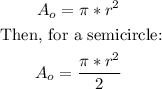
Therefore, for a semicircle with a radius of 5cm:

`\begin{gathered} A_o=(\pi *5^2)/(2) \\ A_o=(25)/(2)\pi \end{gathered}`

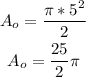
The area of the sector is given as:

`\begin{gathered} A_{\text{ sector}}=((\theta)/(360))*\pi *r^2 \\ \text{ arc length=r*}\theta \end{gathered}`

Given the arc length and the radius, solve for the angle:

`\begin{gathered} 20=10\theta \\ \theta=(20)/(10) \\ \theta=2\text{ degrees} \end{gathered}`

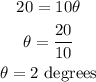
Now, for the area of the sector:

`\begin{gathered} Area_(sector)=((2)/(360))*\pi *10^2 \\ Area_(sector)=(5)/(9)\pi \end{gathered}`