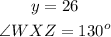The Solution:
Given:
In both figures, we are asked to find the unknown and the given angles.
Question(9):
By the Alternate Angles theorem,
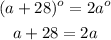
Subtract a from both sides, we get
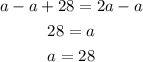
To find angle MNP.
Substitute 28 for a in (a+28).
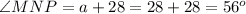
Thus, the correct answers are:
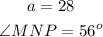
Question (10):
Again, by the Alternate Angles theorem,
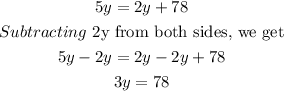
Dividing both sides by 3, we get
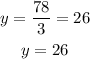
Now, find angle WXZ.
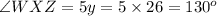
Therefore, the correct answers are: