Question

A 200 g block on a 50-cm-long string swings in a circle on ahorizontal, frictionless table at 75 rpm.a. What is the speed of the block?b. What is the tension in the string?

Answer 1

Given:

The mass of the block, m=200 g=0.2 kg

The length of the string, L=50 cm=0.5 m

The frequency of rotation of the block, f=75 rpm

To find:

a. Speed of the block.

b. The tension in the string.

Step-by-step explanation:

The angular velocity of the block is,

`\omega=(2\pi f)/(60)`

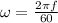
On substituting the known values,

`\begin{gathered} \omega=(2\pi*75)/(60) \\ =7.85\text{ rad/s} \end{gathered}`

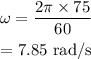
a.

The speed of the block is given by,

`v=\omega r`

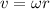
On substituting the known values,

`\begin{gathered} v=7.85*0.50 \\ =3.93\text{ m/s} \end{gathered}`

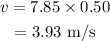
b.

The tension in the string provides the neccessary centripetal force required for the block to trace the circular path.

Thus the tension in the string is given by,

`T=(mv^2)/(r)`

On substituting the known value,

`\begin{gathered} T=(0.2*3.93^2)/(0.5) \\ =6.18\text{ N} \end{gathered}`

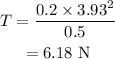
Final answer:

a. The speed of the block is 3.93 m/s

b. The tension in the string 6.18 N