SOLUTION
From the question:
Given:
First-term (a) = 12
n=45
45th term = 144
The formula for finding the nth of an arithmetic series is:
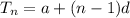
Now, we will substitute the given into the nth term formula to get the common difference for the arithmetic series.
And when we get the common difference, we can then evaluate the arithmetic series:
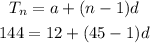

Now, we know the common difference between the terms, we can get the second, third, fourth, fifth term up till the last.

![undefined]()