1. The given polynomial is:
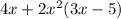
Start by applying the distributive property:
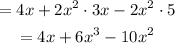
Now, rearrange the terms so that they're written in descending order of exponent:
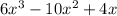
The degree of a polynomial is given by the largest exponent, then its degree is 3 and the number of terms is 3.
2. Polynomial:
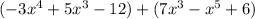
Start by combining like terms:

And rearrange the terms in descending order of exponent:
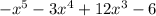
The degree is 5 and the number of terms is 4.
3. Polynomial:
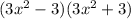
It is the factored form of the difference of two squares:
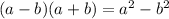
By replacing the known values we have:
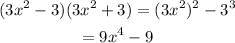
Then the degree is 4 and the number of terms is 2.