The answer is
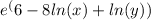 .
.
Use the properties of logarithms to write the following expression as a single term that doesn't contain a logarithm.
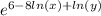
To answer this question, we can use the following properties of logarithms:
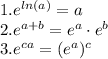
Using these properties, we can rewrite the given expression as follows:
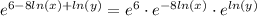
We can then use property 3 to simplify the expression further:
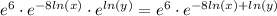
Finally, we can use property 1 to simplify the expression to a single term:
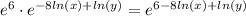
Therefore, the answer to the question is
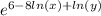 .
.