Looking to receive assistance on the following problem, thank you!Part a.

Question

asked Feb 18, 2023 67.3k views

1 Answer

Mandrake · Answer 1 · 2023-02-24T17:24:49+0000

Given the vectors:

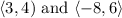
$\langle3,4)\text{ and }\langle-8,6\rangle$

You need to remember that two vectors are parallel when they have their slopes (in Component Form) are equal.

Then, knowing that:

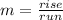
You need to find the slope of each vector:

- The slope of the first vector is:

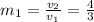
$m_1=\frac{v_2_{}}{v_1_{}_{}}=(4)/(3)$

- The slope of the second vector is:

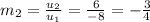
$m_2=\frac{u_2_{}}{u_1_{}}=(6)/(-8)=-(3)/(4)$

Since:

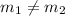
$m_1\\e m_2$

The vectors are not parallel.

To find if they are orthogonal, you need to know that, if:

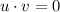
$u\cdot v=0$

The vectors are orthogonal.

Then, it is important to remember that:

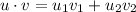
$u\cdot v=u_1v_1+u_2v_2$

You can set up that:

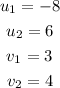
$\begin{gathered} u_1=-8 \\ u_2=6 \\ v_1=3_{} \\ v_2=4 \end{gathered}$

Substituting values and evaluating, you get:

$u\cdot v=(-8)(3)+(6)(4)=-24+24=0$

Therefore, they are orthogonal.

Hence, the answer is: Orthogonal.