Question

A certain mass of a gas occupies a volume of 85.0 L at a pressure of 95.0 kPa anda temperature of 55.0 °C. What will be its Celsius temperature when its volume is6,50 L and its pressure is 130 kPa?

Answer 1

This is a combined gas law problem. Let's see the formula of combined gas law:

`(P_1V_1)/(T_1)=(P_2V_2)/(T_2),`

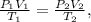
where P is pressure, V is volume and T is temperature. In this formula, the units of each variable must be: for pressure, atm, for volume, in liters (L), and for temperature, in kelvin (K).

Remember that 1 kPa is 0.0986 atm, and kelvin is calculated summing 273 for celsius.

Let's calculate pressure:

`P_1=95.0\text{ kPa}\cdot\frac{0.0986\text{ atm}}{1\text{kPa}}=0.94\text{ atm.}`

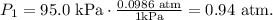
And the formula for temperature in kelvin is:

`T=^oC+273.`

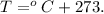
For our initial temperature, we have:

`T_1=55.0^oC+273=328K\text{.}`

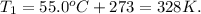
So, the initial data will be:

`P_1=0.94atm,V_1=85\text{ L},T_1=328K\text{.}`

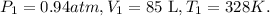
Now, let's do the conversions for the final data. For pressure, we have:

`P_2=130kPa\cdot\frac{0.0986\text{ atm}}{1\text{ kPa}}=1.283\text{ atm.}`

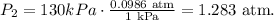
So, our final data is:

`P_2=\text{1.283 atm, }V_2=6.50L,T_2=?`

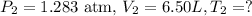
The problem is asking for the temperature in Celsius.

The first step is clear temperature (2) of the formula of combined gas law that is at the beginning:

`T_2=(P_2\cdot V_2\cdot T_1)/(P_1\cdot V_1),`

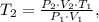
Then, you have to replace the given data, like this:

`T_2=\frac{1.283\text{ atm}\cdot6.50L\cdot328K}{0.94\text{ atm}\cdot85L}=34.23K,`

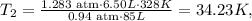
But remember that this answer is in kelvin, so now, we need to clear the formula of temperature to obtain the result in Celsius. The formula is:

`T\text{ =K}-273.`

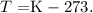
And replacing the result, we can calculate the temperature in Celsius, like this:

`T_2=34.23-273=-238.8^oC.`

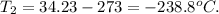
So, the answer will be -238.8 C, because when volume decreases, the temperature decreases (volume and temperature are directly proportional), and when pressure is increasing, the temperature decreases (pressure and temperature are inversely proportional).