Question

Which set of integers does not represent the length of the sides of a triangle

Answer 1

Consider that any three sides can form a triangle only if the following condition is satisfied,

`\text{ Largest Side}<\text{ Sum of other two sides}`

Now, we have to check this condition for each of the given options.

Consider the option A,

`\begin{gathered} 12<4+8 \\ 12<12 \end{gathered}`

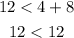
Clearly, the obtained result is a false statement. The given set of values does not satisfy the condition, so they cannot form a triangle.

Consider the option B,

`\begin{gathered} 11<9+10 \\ 11<19 \end{gathered}`

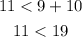
The obtained result is a true statement. The given set of values satisfy the condition, so they will definitely form a triangle.

Consider the option C,

`\begin{gathered} 9<7+4 \\ 9<11 \end{gathered}`

The obtained result is a true statement. The given set of values satisfy the condition, so they will definitely form a triangle.

Consider the option D,

`\begin{gathered} 11<6+6 \\ 11<12 \end{gathered}`

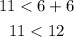
The obtained result is a true statement. The given set of values satisfy the condition, so they will definitely form a triangle.

Thus, it can be concluded that only the set of values in option A will not form a triangle.

Therefore, option A is the correct choice.