Consider that any three sides can form a triangle only if the following condition is satisfied,
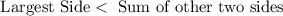
Now, we have to check this condition for each of the given options.
Consider the option A,
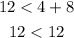
Clearly, the obtained result is a false statement. The given set of values does not satisfy the condition, so they cannot form a triangle.
Consider the option B,
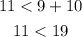
The obtained result is a true statement. The given set of values satisfy the condition, so they will definitely form a triangle.
Consider the option C,
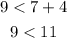
The obtained result is a true statement. The given set of values satisfy the condition, so they will definitely form a triangle.
Consider the option D,
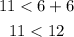
The obtained result is a true statement. The given set of values satisfy the condition, so they will definitely form a triangle.
Thus, it can be concluded that only the set of values in option A will not form a triangle.
Therefore, option A is the correct choice.