Solution
Minimum:
- The minimum is gotten from the value with a stem of 1. The smallest leaf on this stem is 4.
- Thus, the minimum is 14
Q1:
- The first quartile position is gotten using the formula below:
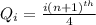
- Thus, the quartile position is:
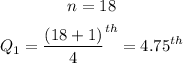
- Thus, the first quartile is between the 4th and 5th position. This is between 23 and 27.
- To find the correct first quartile, we use the formula below:
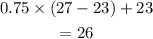
- Thus, Q1 = 26
Median
- The median is gotten below:
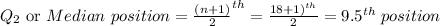
- Thus, the Median is between 41 and 44.
- The median is simply the average of both numbers done below:
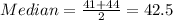
Q3:
- This is the same process as finding Q1. This is done below:
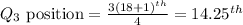
- The Q3 is between 54 and 54.
- Thus, the Q3 is 54 since the Q3 is between the same number
Maximum:
- The maximum value is gotten from the stem with the largest value. The leaf of this stem will be the maximum value of the entire dataset.
- Thus the maximum is 63