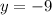Solution:
The equation of a line passing through two points is expressed as

Given that the line passes through the points (7,-9) and (9,-9), this implies that
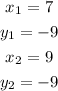
step 1: Evaluate the slope of the line.
Recall that the slope of the line is expressed as
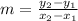
Thus, the slope is evaluated to be
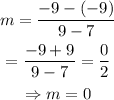
Thus, the slope of the line is zero.
step 2: Express the equation of the line.
Since the slope of the line is evaluated to be zero, we have
![\begin{gathered} y-y_(1)=m(x-x_(1)) \\ \Rightarrow y-\left(-9\right)=0\left(x-7\right) \\ open\text{ parentheses,} \\ y+9=0\text{ ---- equation 3} \\ \end{gathered}]()
In slope intercept form, the equation is expressed as

Thus, from equation 3, the equation in slope-intercept form becomes
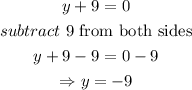
Hence, the equation of the line in slope-intercept form is